坐标系、向量

http://candycat1992.github.io/unity_shaders_book/unity_shaders_book_chapter_4.pdf

笛卡尔坐标系

笛卡尔坐标系（Cartesian Coordinate System）

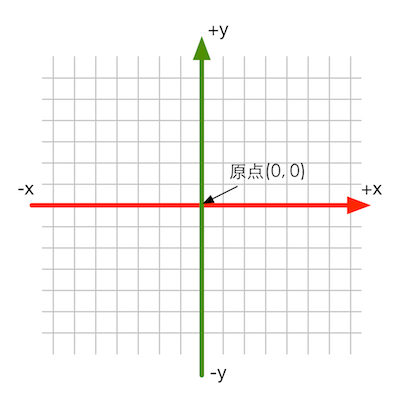
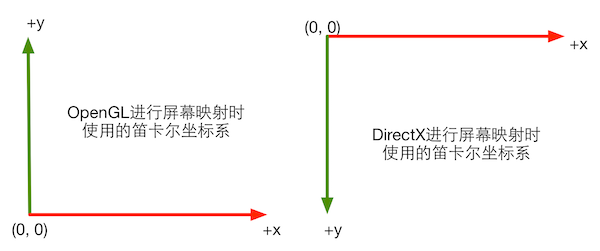
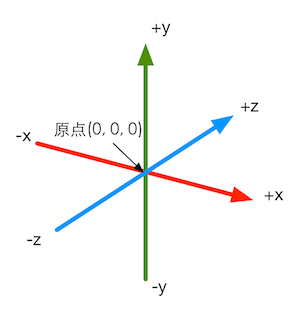
基矢量（basis vector）：三维笛卡尔坐标系的三个坐标轴。

标准正交基（orthonormal basis）：基矢量相互垂直且长度为1。

正交基（orthogonal basis）：坐标系中坐标轴之间相互垂直但长度不为1.

左手坐标系（left-handed coordinate space）、右手坐标系（right-handed coordinate space）

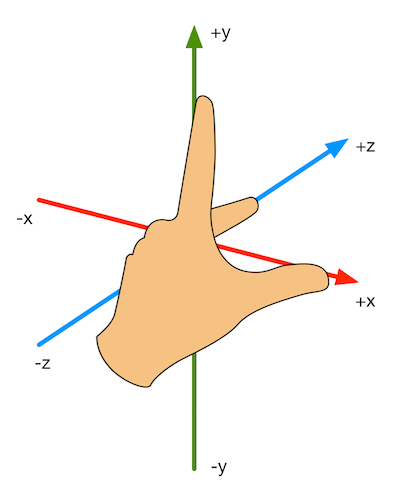
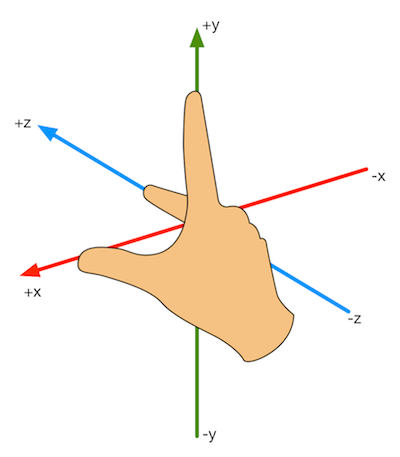
同一种坐标系有相同的旋向性（handedness）

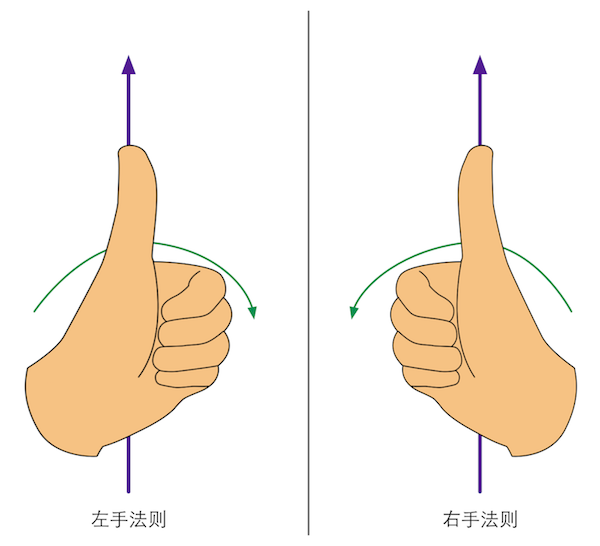
左手法则（left-hand rule）、右手法则（right-hand rule）：在左手坐标系中，举起左手，握拳，伸出大拇指指向旋转轴的正方向，剩下4个手指弯曲的方向就是旋转的正方向。右手坐标系使用相似的判断方法。

Unity的坐标系

在模型空间和世界空间中，Unity使用的是左手坐标系。

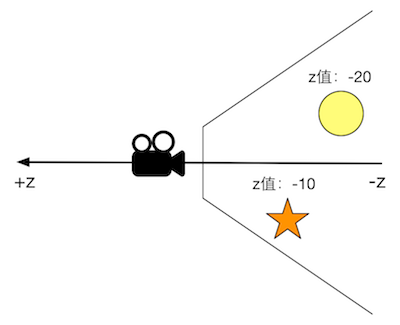
在观察空间中，Unity使用的是右手坐标系。观察空间就是以摄像机为原点的坐标系，摄像机的前向是Z轴的负方向，Z轴越小，物体的深度越大，离摄像机越远。

点和矢量

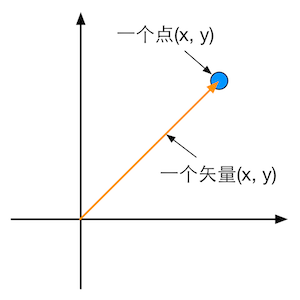
矢量（vector）是n维空间中一种包含了模（magnitude）和方向（direction）的有向线段。它是为了和标量（scalar）区分开来提出的。标量是只有模没有方向。

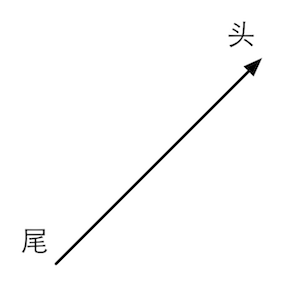
矢量的头（head）指的是箭头所在的端点处，尾（tail）指的是另一个端点。矢量被用于表示相对于某个点的偏移（displacement）。

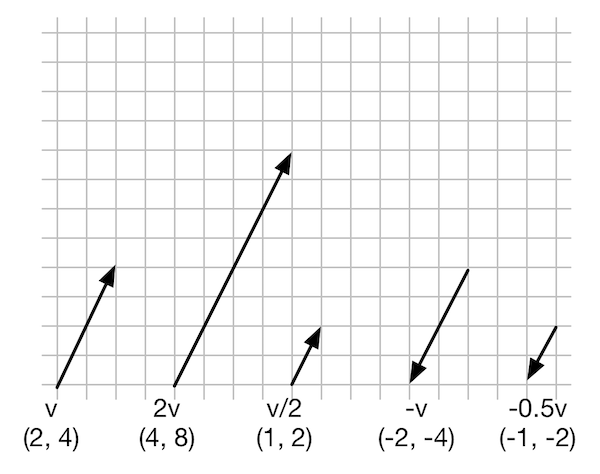
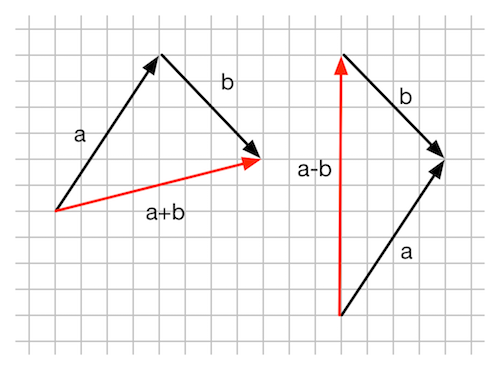
矢量的加减

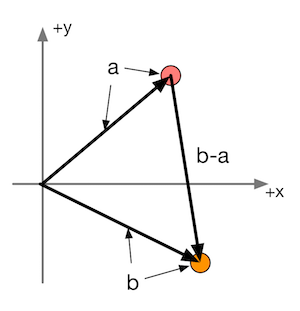
三角形定则（triangle rule）：矢量尾对尾，指向被减者；矢量头对头，指向减者。

矢量的模（magnitude）

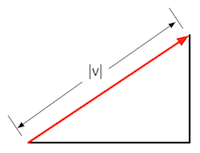
单位矢量（unit vector）

也被称为归一化的矢量（normalized vector)。

矢量的点积（dot product）

矢量的点积满足交换律，它的结果是一个标量，矢量点积的几何意义是投影（projection）。

点积的符号：

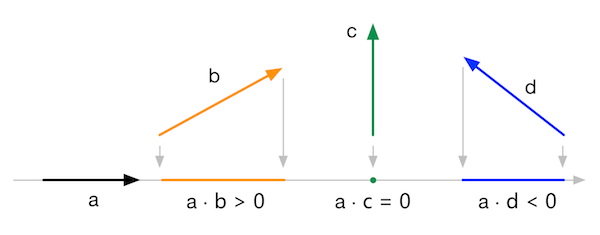
矢量的叉积（cross product）

矢量的叉积不满足交换律，也不满足结合律，但是满足反交换律，它的结果是一个矢量。

三维矢量叉积的计算规律。不同颜色的线表示了计算结果矢量中对应颜色的分量的计算路径。以红色为例，即结果矢量的第一个分量，它是从第一个矢量的y分量出发乘以第二个矢量的z分量，再减去第一个矢量的z分量和第二矢量的y分量的乘积

叉积最常见的应用就是计算垂直于一个平面、三角形的矢量。还可以用于判断三角面片的朝向。